SP#7: Unit Q Concept 2: Finding All Trig Functions When Given One Trig Function and Quadrant

Please see my SP 7, made in collaboration with Brian Chuong, by visiting their blog here. Also, be sure to check out the other awesome posts on their blog.

I/D #3: Unit Q - Pythagorean Identities.

Inquiry Summary Activity:

1) sin²x + cos²x = 1 is derived from the Pythagorean Theorem, which is, x² + y² = r².


When we divide r² from both sides, we get "1" on the right, and (x² / r²) + (y² / r²) = 1. We can make this into (x / r)² + (y / r)² = 1. We know that x/ r is sine, and y/r is cosine, so therefore we have sin²x + cos²x = 1.

2)

In the first picture, you divide cosine from each side, and end up with cos²x / cos²x + sin²x / cos²x = 1/ cos²x. this simplifies into 1 + tan²x = sec²x, and the second one is divided by sine, and you end up with 1 + cot²x = csc²x

Inquiry Activity Reflection

1) I connections that I see between Units N, O, P, and Q so far are that they all relate to one another. We start off by using the unit circle, then we basically derive the identities using the proofs in concept Q.

2) If I had to describe trigonometry in THREE words, they would be: Just Keep Practicing.

WPP #13/14: Unit P Concepts 6-7 - The Laws of Sine and Cosine

Please see my WPP 13-14, made in collaboration with Brian Chuong, by visiting their blog here. Also, be sure to check out the other awesome posts on their blog.

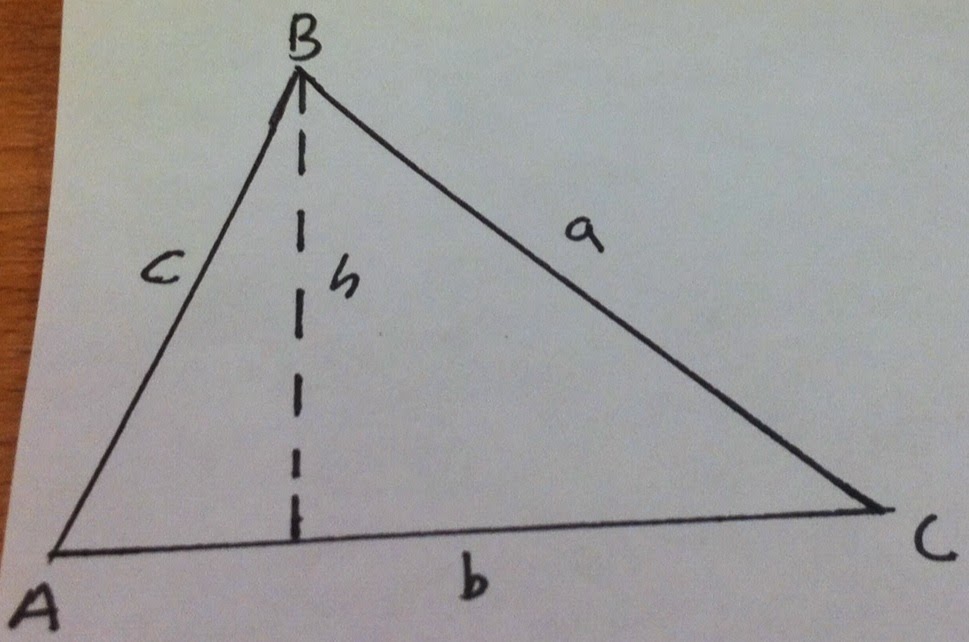
BQ#1 Unit P Concept 2 and 4

Law of Sines:

-Why do we need the need the Law of Sines?

We need the Law of Sines because it lets us solve non-right triangles.

-How is it derived from what we know?

When we are given something other than a non-triangle, we are faced with the challenge of being able to solve it. Because of that, we have to use the Law of Sines

The first step towards deriving the Law of Sines is to draw a line perpendicular to side b. Since we don't have a right triangle, we have to make one if we want to derive the law.

Now that we have two right triangles, we need a trigonometric function that involves the opposite of either A or C, and the hypotenuse. This being the Law of SINES, the function just so happens to be sine.

Since Sine is Opposite/Hypotenuse, we have sin C = h/a and sin A = h/a

In order to find h, we need to multiply c and a to both sides (of their respective equations). When we do this, we have a*sin*C = h and c*sin*A = h. Since both of the equations are equal to side "h", we can set them equal to each other.

When we set them equal to each other, we can divide both sides "c" and "a" in order to cancel them out and get the Law.

After you divide "c" and "a", you are left with sinC/c = sinA/a.

Area of an Oblique Triangle

In this triangle, you draw a line perpendicular from angle B to line b. In order to get your right triangle in order to find the area of the oblique triangle.

Like in the Law of Sines,  you take the Sine of C, in order to derive the are of the oblique triangle.

Once you take the Sine, then you multiply a to both sides, and get h = a*sin*C. Since you have an answer to what "h" is, then you plug h into the original area equation. The original equation is A = 1/2*b*h, then you have A = 1/2 b*(a*sin*C).

How does it Relate to the Original Equation:

This equation relates to the original equation, because the only thing that changes, is that you find the value of one of the variables, and then plug it into the original. 

WPP #12: Unit O Concept 10 - Solving Angle of Elevation and Depression Word Problem

Mark is spending a glorious weekend away from school, and is indulging in music. At a local venue, Mark's band was invited to play with multiple other local bands. When they arrive at the venue, Mark can't help but realize that the building is quite tall. 

A) If Mark is standing 10 feet away from the building, how tall is the building itself if the angle of elevation is 50 degrees?

B) Mark is now standing on top of the building. He looks across the street, and sees that the restaurant across the street has tables outside. In the starry night, his gaze is captured by a rather extremely attractive girl who appears to be his age and is sitting the equivalent of 30 feet away from him if he were to zip line over to her. Being the geek he is, the first thing that comes to Mark's mind is "How far away might this lady be?" (angle of depression is 40 degrees)

The Solution

I/D2: Unit O - How can we derive the patterns for our special right triangles?

Inquiry Activity Summary

1) 30-60-90 Triangle

In order to derive the 30-60-90 from an equilateral triangle whose sides all equal 1 (in this case), we start out by cutting it straight down the middle (vertically) in a way that the triangle becomes two identical triangles. Original, the triangle is made up of all 60 degree angles. By cutting it in half, the top angle become 30 degrees, and either the right or left angle (depending on which one you use) is the 60 degree angle, thus giving you the 30-60-90 Triangle.

In the last three pictures, you can see the way that the 30-60-90 triangle is formed. We know that each leg should be equal to 1, but we have one side that has to values of 1/2 when it is split. This is simply to show that when we split the triangle down the middle, you end up with 2 separate 30-60-90 triangles with legs being equal to 1, 1/2, and the b leg is equal to radical 3/2. The way you find the value of leg b is shown in the next picture.

Here, we have the Pythagorean Theorem. As you can see, we have 1/2 to the second power. This gives us 1/4, which we subtract from 1 on the other side. we are left with radical 3/4 which then simplifies to radical 3 divided by 2. 

Here, we have the 30-60-90 triangle, but we have placed "n" in each value to show that there is a proportion in the triangle. The values of each leg form a ratio, which remains the same regardless of what value you use for n. Since you multiply fairly, you multiply the same amount for "n", thus ending up with the same ratio you started with.

2) 45-45-90 triangle

In order to obtain this triangle from a square, we have to cut the square diagonally. Since we start out with a square, all sides are equal to 1 (the given value), and we simply need to find the value of the hypotenuse.

In these two last pictures, we see the transformation from the square to the triangle. Using what we know of the 45-45-90 triangle, we know that by cutting the square diagonally, your 90 degree angles in two of the corners will split in half to give you the 45 degree angles that we need. Then, we know that the legs directly opposite to the 45 degree angles are "n", which means that n=1 (since legs=1). We know that the leg opposite to the 90 degree angle is n radical 2, which means that the hypotenuse is radical 2.

This picture goes over the way to get the hypotenuse using Pythagorean Theorem. You get the same answer, but have a couple extra steps.

This picture shows the original square, with substituted into the values. Like stated in the 30-60-90, we use the letter "n" to show the ratio between all the legs, and just like in the 30-60-90 triangle, this ratio is the same regardless of what value you substitute for "n".

Inquiry Activity Reflection

Something I never noticed before about special right triangles is that you can derive them from either a square or a triangle of same values.

Being able to derive these patterns myself aids in my learning because I can quickly derive the Special Right Triangles during a test if I forget all else, and possibly pass the test.