BQ#1 Unit P Concept 2 and 4

Law of Sines:

-Why do we need the need the Law of Sines?

We need the Law of Sines because it lets us solve non-right triangles.

-How is it derived from what we know?

When we are given something other than a non-triangle, we are faced with the challenge of being able to solve it. Because of that, we have to use the Law of Sines

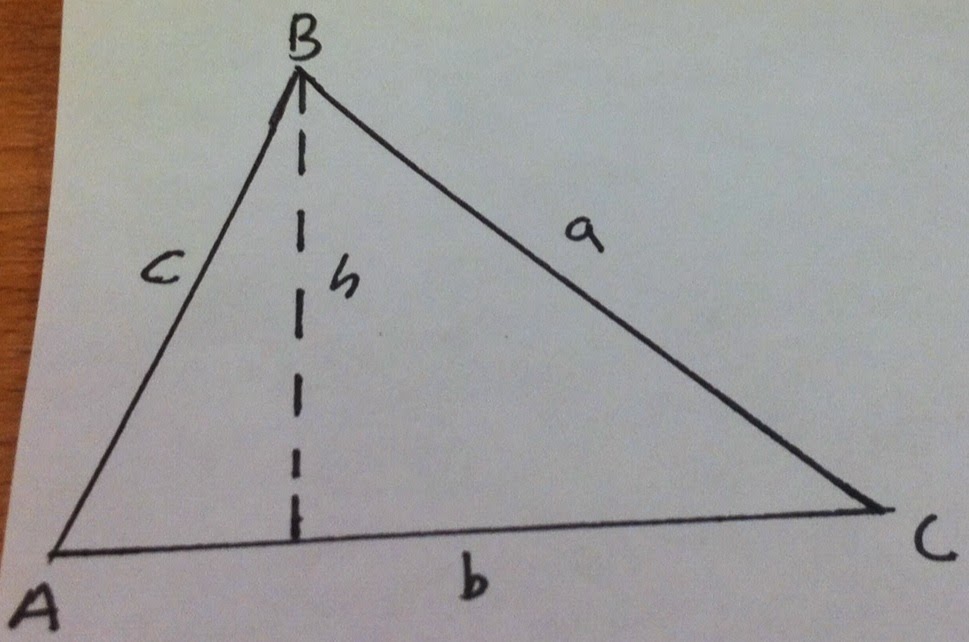
The first step towards deriving the Law of Sines is to draw a line perpendicular to side b. Since we don't have a right triangle, we have to make one if we want to derive the law.

Now that we have two right triangles, we need a trigonometric function that involves the opposite of either A or C, and the hypotenuse. This being the Law of SINES, the function just so happens to be sine.

Since Sine is Opposite/Hypotenuse, we have sin C = h/a and sin A = h/a

In order to find h, we need to multiply c and a to both sides (of their respective equations). When we do this, we have a*sin*C = h and c*sin*A = h. Since both of the equations are equal to side "h", we can set them equal to each other.

When we set them equal to each other, we can divide both sides "c" and "a" in order to cancel them out and get the Law.

After you divide "c" and "a", you are left with sinC/c = sinA/a.

Area of an Oblique Triangle

In this triangle, you draw a line perpendicular from angle B to line b. In order to get your right triangle in order to find the area of the oblique triangle.

Like in the Law of Sines,  you take the Sine of C, in order to derive the are of the oblique triangle.

Once you take the Sine, then you multiply a to both sides, and get h = a*sin*C. Since you have an answer to what "h" is, then you plug h into the original area equation. The original equation is A = 1/2*b*h, then you have A = 1/2 b*(a*sin*C).

How does it Relate to the Original Equation:

This equation relates to the original equation, because the only thing that changes, is that you find the value of one of the variables, and then plug it into the original.